第 6 章 拉普拉斯变换

许多实际工程问题涉及受到不连续或脉冲强制项作用的机械系统和电气系统。对于这些问题，第 3 章中描述的方法通常使用起来相当笨拙。另一种特别适合于这些问题的方法，尽管更普遍地有用，是基于拉普拉斯变换。在本章中，我们将描述这种重要方法的工作原理，重点是工程应用中出现的典型问题。

6.1 拉普拉斯变换的定义

反常积分。由于拉普拉斯变换涉及从零到无穷的积分，因此有必要了解这种类型的反常积分，以便理解后续的变换性质发展。我们在此提供对此类反常积分的简要回顾。如果您已经熟悉反常积分，您可以跳过此回顾。另一方面，如果反常积分对您来说是新的，那么您应该查阅微积分书籍，您将在其中找到更多细节和示例。

在无界区间上的反常积分定义为有限区间上积分的极限；因此

∫a∞f(t)dt=lim⁡A→∞∫aAf(t)dt\begin{equation*} \int_{a}^{\infty} f(t) d t=\lim _{A \rightarrow \infty} \int_{a}^{A} f(t) d t \tag{1} \end{equation*}

其中 AA 是一个正实数。如果从 aa 到 AA 的定积分对于每个 A>aA>a 都存在，并且如果当 A→∞A \rightarrow \infty 时这些值的极限存在，则称该反常积分收敛到该极限值。否则，该积分被称为发散，或不存在。以下示例说明了这两种可能性。

示例 1

反常积分 ∫1∞dtt\int_{1}^{\infty} \frac{d t}{t} 是发散还是收敛？

解：

从方程 (1) 我们得到

∫1∞dtt=lim⁡A→∞∫1Adtt=lim⁡A→∞ln⁡A\int_{1}^{\infty} \frac{d t}{t}=\lim _{A \rightarrow \infty} \int_{1}^{A} \frac{d t}{t}=\lim _{A \rightarrow \infty} \ln A

由于 lim⁡A→∞ln⁡A=∞\lim _{A \rightarrow \infty} \ln A=\infty，因此反常积分发散。

示例 2

计算反常积分 ∫0∞ectdt\int_{0}^{\infty} e^{c t} d t。对于 cc 的哪些值，这个反常积分收敛？

解：

假设 cc 是一个实非零常数。那么

∫0∞ectdt=lim⁡A→∞∫0Aectdt=lim⁡A→∞ectc∣0A=lim⁡A→∞1c(ecA−1)\begin{aligned} \int_{0}^{\infty} e^{c t} d t & =\lim _{A \rightarrow \infty} \int_{0}^{A} e^{c t} d t=\left.\lim _{A \rightarrow \infty} \frac{e^{c t}}{c}\right|_{0} ^{A} \\ & =\lim _{A \rightarrow \infty} \frac{1}{c}\left(e^{c A}-1\right) \end{aligned}

由此可见，如果 c<0c<0，则反常积分收敛到值 −1/c-1 / c，如果 c>0c>0，则发散。如果 c=0c=0，则被积函数 ecte^{c t} 是值为 1 的常数函数。在这种情况下

lim⁡A→∞∫0A1dt=lim⁡A→∞(A−0)=∞\lim _{A \rightarrow \infty} \int_{0}^{A} 1 d t=\lim _{A \rightarrow \infty}(A-0)=\infty

所以积分再次发散。

示例 3

找到使反常积分 ∫1∞t−pdt\int_{1}^{\infty} t^{-p} d t 收敛的所有实数 pp。对于 pp 的哪些值，它发散？

解：

假设 pp 是一个实常数且 p≠1p \neq 1；情形 p=1p=1 在示例 1 中考虑过。那么

∫1∞t−pdt=lim⁡A→∞∫1At−pdt=lim⁡A→∞11−p(A1−p−1)\int_{1}^{\infty} t^{-p} d t=\lim _{A \rightarrow \infty} \int_{1}^{A} t^{-p} d t=\lim _{A \rightarrow \infty} \frac{1}{1-p}\left(A^{1-p}-1\right)

当 A→∞A \rightarrow \infty 时，如果 p>1p>1，则 A1−p→0A^{1-p} \rightarrow 0，但如果 p<1p<1，则 A1−p→∞A^{1-p} \rightarrow \infty。因此，对于 p>1p>1，∫1∞t−pdt\int_{1}^{\infty} t^{-p} d t 收敛到值 1/(p−1)1 /(p-1)，但对于 p≤1p \leq 1（包含示例 1 的结果）发散。这些结果类似于无穷级数 ∑n=1∞n−p\sum_{n=1}^{\infty} n^{-p} 的结果。

在讨论 ∫a∞f(t)dt\int_{a}^{\infty} f(t) d t 可能存在性之前，定义一些术语是有帮助的。如果区间 1{ }^{1} 可以被有限数量的点 α=t0<t1<⋯<tn=β\alpha=t_{0}<t_{1}<\cdots<t_{n}=\beta 分割，使得

  1. ff 在每个开子区间 ti−1<t<tit_{i-1}<t<t_{i} 上是连续的。
  2. 当从子区间的内部接近每个子区间的端点时，ff 接近一个有限极限。

换句话说，如果 ff 在 α≤t≤β\alpha \leq t \leq \beta 上是分段连续的，则除了有限数量的跳跃不连续点之外，它在那里是连续的。如果 ff 在 α≤t≤β\alpha \leq t \leq \beta 上对于每个 β>α\beta>\alpha 都是分段连续的，则称 ff 在 t≥αt \geq \alpha 上是分段连续的。图 6.1.1 显示了一个分段连续函数的示例。

分段连续函数在有限区间上的积分只是由分割点创建的子区间上积分的和。例如，对于函数 f(t)f(t)

[^0]

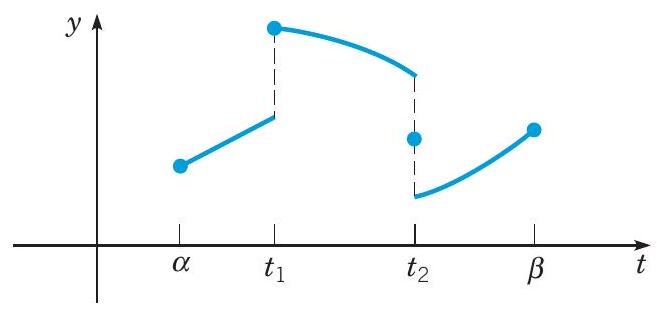
图 6.1.1 一个分段连续函数 y=f(t)y=f(t)。 在图 6.1.1 中所示的函数，我们有

∫αβf(t)dt=∫αt1f(t)dt+∫t1t2f(t)dt+∫t2βf(t)dt\begin{equation*} \int_{\alpha}^{\beta} f(t) d t=\int_{\alpha}^{t_{1}} f(t) d t+\int_{t_{1}}^{t_{2}} f(t) d t+\int_{t_{2}}^{\beta} f(t) d t \tag{2} \end{equation*}

对于图 6.1.1 中所示的函数，我们已将值赋给函数在端点 α\alpha 和 β\beta 以及分割点 t1t_{1} 和 t2t_{2} 处的值。然而，就方程 (2) 中的积分而言， f(t)f(t) 是否在这些点上定义，或者在这些点上赋予 f(t)f(t) 什么值，都无关紧要。无论如何，方程 (2) 中的积分值保持不变。

因此，如果 ff 在区间 a≤t≤Aa \leq t \leq A 上是分段连续的，则 ∫aAf(t)dt\int_{a}^{A} f(t) d t 存在。因此，如果 ff 对于 t≥at \geq a 是分段连续的，则对于每个 A>aA>a ， ∫aAf(t)dt\int_{a}^{A} f(t) d t 存在。然而，正如前面的例子所示，分段连续性不足以确保反常积分 ∫a∞f(t)dt\int_{a}^{\infty} f(t) d t 的收敛性。

如果 ff 不能用初等函数轻易积分，那么应用 ∫a∞f(t)dt\int_{a}^{\infty} f(t) d t 的收敛性定义可能很困难。通常，测试反常积分收敛或发散的最方便方法是使用以下比较定理，该定理类似于无穷级数的类似定理。

定理 6.1.1

如果 ff 对于 t≥at \geq a 是分段连续的，如果对于某个正的常数 MM，t≥Mt \geq M 时，有 ∣f(t)∣≤g(t)|f(t)| \leq g(t)，并且如果 ∫M∞g(t)dt\int_{M}^{\infty} g(t) d t 收敛，则 ∫a∞f(t)dt\int_{a}^{\infty} f(t) d t 也收敛。

另一方面，如果对于 t≥Mt \geq M，f(t)≥g(t)≥0f(t) \geq g(t) \geq 0，并且如果 ∫M∞g(t)dt\int_{M}^{\infty} g(t) d t 发散，则 ∫a∞f(t)dt\int_{a}^{\infty} f(t) d t 也发散。

这里不给出这些微积分结果的证明。然而，通过比较 ∫M∞g(t)dt\int_{M}^{\infty} g(t) d t 和 ∫M∞∣f(t)∣dt\int_{M}^{\infty}|f(t)| d t 所代表的面积，使它们看起来是合理的。用于比较目的的最有用的函数是 ecte^{c t} 和 t−pt^{-p}，我们在例 1、2 和 3 中考虑了它们。

拉普拉斯变换。积分变换是求解线性微分方程非常有用的工具之一。积分变换是以下形式的关系

F(s)=∫αβK(s,t)f(t)dt\begin{equation*} F(s)=\int_{\alpha}^{\beta} K(s, t) f(t) d t \tag{3} \end{equation*}

其中 K(s,t)K(s, t) 是给定的函数，称为变换的核，积分的上下限 α\alpha 和 β\beta 也是给定的。α=−∞\alpha=-\infty 或 β=∞\beta=\infty 或两者都成立是有可能的。关系式 (3) 将函数 ff 转换为另一个函数 FF，它被称为 ff 的变换。

有几种积分变换在应用数学中很有用，但在本章中，我们只考虑拉普拉斯变换2{ }^{2}。此变换定义如下

[^1]所示。令 f(t)f(t) 在 t≥0t \geq 0 时给定，并假设 ff 满足稍后将要说明的某些条件。那么，ff 的拉普拉斯变换（我们将其表示为 L{f(t)}\mathcal{L}\{f(t)\} 或 F(s)F(s)）由以下等式定义

$$

L{f(t)}=F(s)=∫0∞e−stf(t)dt\begin{equation*} \mathcal{L}\{f(t)\}=F(s)=\int_{0}^{\infty} e^{-s t} f(t) d t \tag{4} \end{equation*}

$$ 只要这个反常积分收敛。拉普拉斯变换使用核 K(s,t)=e−stK(s, t)=e^{-s t}。由于具有常系数的线性微分方程的解基于指数函数，因此拉普拉斯变换对于此类方程特别有用。使用拉普拉斯变换求解微分方程的一般思路如下：

  1. 使用关系式 (4) 将 tt 域中未知函数 ff 的初值问题转换为 ss 域中 FF 的更简单的问题（实际上是一个代数问题）。
  2. 求解这个代数问题以找到 FF。
  3. 从其变换 FF 中恢复所需的函数 ff。最后一步被称为“反变换”。

一般来说，参数 ss 可能是复数，并且只有当我们把 F(s)F(s) 看作复变量的函数时，拉普拉斯变换的全部能力才能发挥出来。但是，对于此处讨论的问题，仅考虑 ss 的实数值就足够了。

如果函数 ff 满足某些条件（例如以下定理中陈述的那些条件），则 ff 的拉普拉斯变换 FF 存在。

定理 6.1.2

假设

(i) 对于任何正数 AA，ff 在区间 0≤t≤A0 \leq t \leq A 上是分段连续的，并且

(ii) 存在实常数 KK，aa 和 MM，KK 和 MM 是正数，使得

∣f(t)∣≤Keat 当 t≥M 时|f(t)| \leq K e^{a t} \text { 当 } t \geq M \text{ 时}

那么，由等式 (4) 定义的拉普拉斯变换 L{f(t)}=F(s)\mathcal{L}\{f(t)\}=F(s) 对 s>as>a 存在。

为了建立这个定理，我们必须证明等式 (4) 中的积分对 s>as>a 收敛。将反常积分分成两部分，我们有

∫0∞e−stf(t)dt=∫0Me−stf(t)dt+∫M∞e−stf(t)dt\begin{equation*} \int_{0}^{\infty} e^{-s t} f(t) d t=\int_{0}^{M} e^{-s t} f(t) d t+\int_{M}^{\infty} e^{-s t} f(t) d t \tag{5} \end{equation*}

定理假设(i)保证了方程(5)右侧的第一个积分存在；因此，F(s)F(s)的存在性取决于第二个积分的收敛性。由假设(ii)，对于t≥Mt \geq M，我们有

∣e−stf(t)∣≤Ke−steat=Ke(a−s)t\left|e^{-s t} f(t)\right| \leq K e^{-s t} e^{a t}=K e^{(a-s) t}

因此，根据定理6.1.1，F(s)F(s)存在的条件是∫M∞e(a−s)tdt\int_{M}^{\infty} e^{(a-s) t} d t收敛。参考例1，用a−sa-s代替cc，我们发现当a−s<0a-s<0时，后一个积分收敛，这就证明了定理6.1.2。

在本章中（第6.5节除外），我们几乎专门处理满足定理6.1.2条件的函数。这些函数被描述为分段连续的，并且当t→∞t \rightarrow \infty时具有指数阶。注意，有些函数当t→∞t \rightarrow \infty时不是指数阶的。一个这样的函数是f(t)=et2f(t)=e^{t^{2}}。当t→∞t \rightarrow \infty时，无论常数KK和aa有多大，该函数的增长速度都比KeatK e^{a t}快。

一些重要基本函数的拉普拉斯变换在以下例子中给出。

示例 4

求L{1}\mathcal{L}\{1\}。

解：

设f(t)=1,t≥0f(t)=1, t \geq 0。然后，如例2所示，

L{1}=∫0∞e−stdt=−lim⁡A→∞e−sts∣0A=1s,s>0\mathcal{L}\{1\}=\int_{0}^{\infty} e^{-s t} d t=-\left.\lim _{A \rightarrow \infty} \frac{e^{-s t}}{s}\right|_{0} ^{A}=\frac{1}{s}, \quad s>0

示例 5

求L{eat}\mathcal{L}\left\{e^{a t}\right\}。 解：

设f(t)=eat,t≥0f(t)=e^{a t}, t \geq 0。然后，再次参考例2，

L{eat}=∫0∞e−steatdt=∫0∞e−(s−a)tdt=1s−a,s>a\begin{aligned} \mathcal{L}\left\{e^{a t}\right\} & =\int_{0}^{\infty} e^{-s t} e^{a t} d t=\int_{0}^{\infty} e^{-(s-a) t} d t \\ & =\frac{1}{s-a}, \quad s>a \end{aligned}

示例 6

求图6.1.2中函数的拉普拉斯变换。

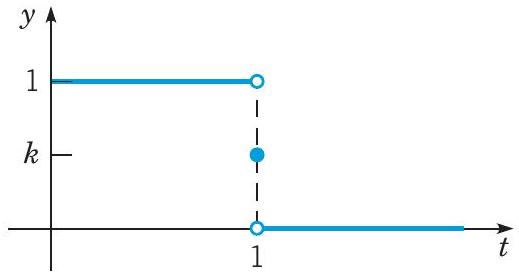
图 6.1.2 例6中分段定义函数的图像。

解：

设

f(t)={1,0≤t<1k,t=10,t>1f(t)= \begin{cases}1, & 0 \leq t<1 \\ k, & t=1 \\ 0, & t>1\end{cases}

其中kk是一个常数。在工程背景下，f(t)f(t)通常表示一个单位脉冲，可能是力或电压。

注意，ff是一个分段连续函数。然后

L{f(t)}=∫0∞e−stf(t)dt=∫01e−stdt=−e−sts∣01=1−e−ss,s>0\mathcal{L}\{f(t)\}=\int_{0}^{\infty} e^{-s t} f(t) d t=\int_{0}^{1} e^{-s t} d t=-\left.\frac{e^{-s t}}{s}\right|_{0} ^{1}=\frac{1-e^{-s}}{s}, \quad s>0

观察到L{f(t)}\mathcal{L}\{f(t)\}不依赖于kk，即间断点处的函数值。即使f(t)f(t)在该点未定义，ff的拉普拉斯变换仍然相同。因此，有许多函数，仅在单个点上的值不同，但具有相同的拉普拉斯变换。

示例 7

求L{sin⁡(at)}\mathcal{L}\{\sin (a t)\}。对于哪些ss值，此变换是定义的？

解：

设f(t)=sin⁡(at),t≥0f(t)=\sin (a t), t \geq 0。然后

L{sin⁡(at)}=F(s)=∫0∞e−stsin⁡(at)dt,s>0.\mathcal{L}\{\sin (a t)\}=F(s)=\int_{0}^{\infty} e^{-s t} \sin (a t) d t, \quad s>0 .

由于

F(s)=lim⁡A→∞∫0Ae−stsin⁡(at)dtF(s)=\lim _{A \rightarrow \infty} \int_{0}^{A} e^{-s t} \sin (a t) d t

通过分部积分，我们得到

F(s)=lim⁡A→∞[−e−stcos⁡(at)a∣0A−sa∫0Ae−stcos⁡(at)dt]=1a−sa∫0∞e−stcos⁡(at)dt\begin{aligned} F(s) & =\lim _{A \rightarrow \infty}\left[-\left.\frac{e^{-s t} \cos (a t)}{a}\right|_{0} ^{A}-\frac{s}{a} \int_{0}^{A} e^{-s t} \cos (a t) d t\right] \\ & =\frac{1}{a}-\frac{s}{a} \int_{0}^{\infty} e^{-s t} \cos (a t) d t \end{aligned}

再次进行分部积分，得到

F(s)=1a−s2a2∫0∞e−stsin⁡(at)dt=1a−s2a2F(s).\begin{aligned} F(s) & =\frac{1}{a}-\frac{s^{2}}{a^{2}} \int_{0}^{\infty} e^{-s t} \sin (a t) d t \\ & =\frac{1}{a}-\frac{s^{2}}{a^{2}} F(s) . \end{aligned}

现在，求解F(s)F(s)，我们有

F(s)=as2+a2,s>0.F(s)=\frac{a}{s^{2}+a^{2}}, \quad s>0 .

在问题5中，您将使用类似的过程来找到L{cos⁡(at)}=ss2+a2\mathcal{L}\{\cos (a t)\}=\frac{s}{s^{2}+a^{2}}，其中s>0s>0。现在，假设f1f_{1}和f2f_{2}是两个函数，它们的拉普拉斯变换分别对于s>a1s>a_{1}和s>a2s>a_{2}存在。然后，对于大于a1a_{1}和a2a_{2}的最大值的ss，

L{c1f1(t)+c2f2(t)}=∫0∞e−st(c1f1(t)+c2f2(t))dt=c1∫0∞e−stf1(t)dt+c2∫0∞e−stf2(t)dt\begin{aligned} \mathcal{L}\left\{c_{1} f_{1}(t)+c_{2} f_{2}(t)\right\} & =\int_{0}^{\infty} e^{-s t}\left(c_{1} f_{1}(t)+c_{2} f_{2}(t)\right) d t \\ & =c_{1} \int_{0}^{\infty} e^{-s t} f_{1}(t) d t+c_{2} \int_{0}^{\infty} e^{-s t} f_{2}(t) d t \end{aligned}

因此

L{c1f1(t)+c2f2(t)}=c1L{f1(t)}+c2L{f2(t)}.\begin{equation*} \mathcal{L}\left\{c_{1} f_{1}(t)+c_{2} f_{2}(t)\right\}=c_{1} \mathcal{L}\left\{f_{1}(t)\right\}+c_{2} \mathcal{L}\left\{f_{2}(t)\right\} . \tag{6} \end{equation*}

方程(6)表明拉普拉斯变换是线性算子，我们在后面会经常使用这个性质。方程(6)中的和可以很容易地推广到任意数量的项。

示例 8

求f(t)=5e−2t−3sin⁡(4t),t≥0f(t)=5 e^{-2 t}-3 \sin (4 t), t \geq 0的拉普拉斯变换。

解：

使用方程(6)，我们写成

L{f(t)}=5L{e−2t}−3L{sin⁡(4t)}\mathcal{L}\{f(t)\}=5 \mathcal{L}\left\{e^{-2 t}\right\}-3 \mathcal{L}\{\sin (4 t)\}

然后，从示例5和7，我们得到

L{f(t)}=5s+2−12s2+16,s>0\mathcal{L}\{f(t)\}=\frac{5}{s+2}-\frac{12}{s^{2}+16}, \quad s>0